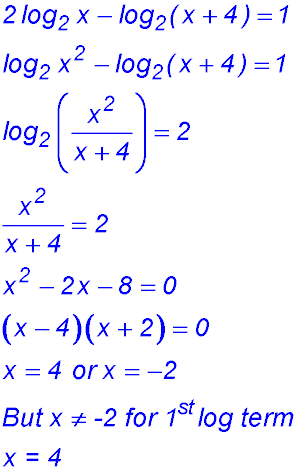Where the techniques of Maths
are explained in simple terms.
Functions - Logarithmic functions - Log laws.
Test Yourself 1 - Solutions.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
| Log laws with numbers. | 1. Simplify log5 2 + log5 10.
|
2. Simplify log3 9 + log7 49.
|
3. Simplify log4 20 - log4 5.
|
4. Simplify 2 log2 8 - 3log6 216.
|
|
| 5. Simplify log5 50 + log5 10 - log5 4.
= log5 50 + log5 10 - log5 4 = log5 (2×52) + log5 2 + log5 5 - log5 22 = log5 2 + 2log5 5 + log5 2 + log5 5 - 2log5 2 = 3log55 = 3 |
6. Simplify log4 20 + (log4 32 - log4 10).
= log4 (4×5) + (log4 (42×2) - log4 (2×5)) = log4 4 + log4 5 + 2log4 4 + log4 2
= 3 |
|
7. Simplify 5log8 2 + 0.5log8 4.
|
8. log10 125 - log10 4 + log10 32
= log10 (125×32÷4) = log10 1000 = log10 103 = 3 |
|
| Log laws with pronumerals. | 9. Simplify log (x + 1) + log (3-x)
log(x + 1)(3 - x). |
10. Simplify log (8x) + log (2x)
log (16x2) |
| 11. Simplify log5 8x - log5 2x
log5 (8x ÷ 2x) = log5 4. |
12. Simplify log10 x2y3 - log10 xy
log10 (x2y3÷xy) = log10 xy2 (= log10 x + 2log10y)
|
|
| 13. Evaluate log4 32 - log4 5 to 3 significant places.
|
14. Find the value of log5 200 - 3log5 2.
|
|
| 15. Simplify 2 log x + 3 log y - log xy2
|
16. Use two approaches to simplify log5 25.
|
|
| 17. Evaluate e(ln2 + ln3)
As the indices are added together, we can form two terms which are multiplied together: eln2 × eln3 = 2 × 3 = 6. |
18. Evaluate e(2 ln4 - 3 ln2)
As indices are subtracted from each other, we can form two terms which are divided:
|
|
| 19. If x = loga 3 and y = loga 5, prove that
LHS = loga a2 - loga 75 = 2loga a - (loga25 + loga 3) = 2 - loga 52 - loga 3 = 2 - 2y - x |
20. Simplify loge (e2 + e) - loge (e+1).
|
|
21. If m = en, show that loge (m2) = 2n.
|
22. Express 3log2 8 in its simplest form.
|
|
23. If e4x = 4, show that  . .
|
24. Simplify log10 20A - log10 2A.
log10 (20A÷2A) = log1010 = 1 |
|
| 25. If a = log12 b and b > 1, which of the following is equivalent to Answer: (b) a = logb 12. Because:
|
26. Which expression is equivalent to 4 + log2 x?
|
|
27. Given that 2log3 (x2y) = 3 + log3 x - log3 y, express y in terms of x.
|
28.
|
|
| Substitutions. | 29. Given loga3 = 1.6 and loga7 = 2.4, find the value of loga (21a).
|
30. Given that log2 5 = 2.32 and that log2 3 = 1.58, find the value of:
|
| 31. Given that loga 2 = 0.4307 and
loga 3 = 0.6826, find the value of loga 24.
|
32. Given that logm p = 1.75 and logm q = 2.25, find the value of
(i) logm (pq) = logmp + logmq = 1.75 + 2.25 = 4.0 (ii) = 1.75 - 2.25 = -0.5 (iii) Let y = pq2 logm y = logm(pq2) = logmp + 2logmq = 1.75 + 2×2.25 = 6.25 So y = m6.25 |
|
33. Given that log3 x = a and log3 y = b, express 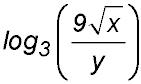 in terms of a and b. in terms of a and b.
|
34. If loga (xy3) = 1 and loga (x2y) = 1, what is the value of loga (xy)?
|
|
| Equations. | 35. Solve 2 loge x = loge (3x + 10).3
|
36. Solve for x:
log5 3 = 2log5 6 + log5 x
|
37. Solve log10(x2) + 3 = log10(x5).
|
38. Solve
log2 (x - 1) = 5 - log2 (x + 3).
|
|
39. Solve log3 (2x - 1) + log3 (x - 4) = 2.
|
40. Solve ln (x + 12) = 2 ln x.
|
|
41. 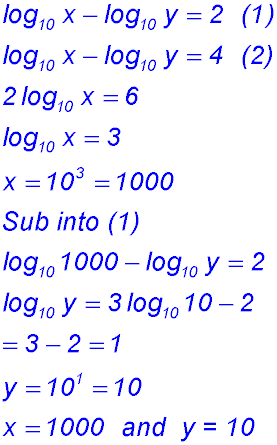 |
42.
|
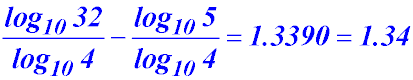
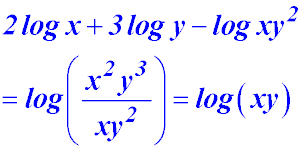
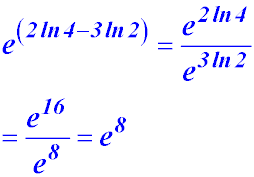
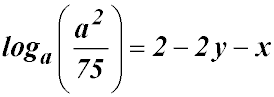 .
.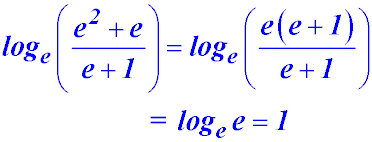
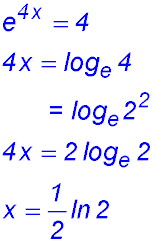
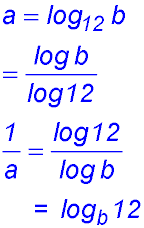
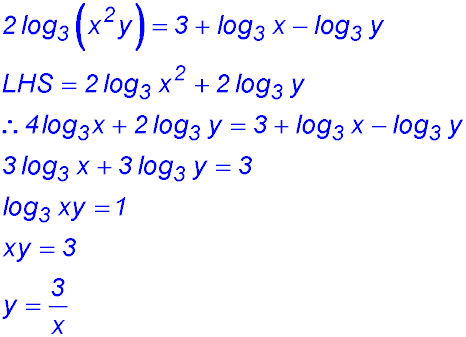
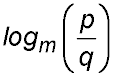 ;
;